数据结构和算法入门
为什么要学习数据结构和算法
1.解决问题的思想
计算机只是一个很冰冷的机器,你给他下发什么样的指令,它就能作出什么样的反应。
而开发工程师要做的是如何把实际的问题转化成计算机的指令,如何转化,来看看《数据结构》的经典说法:
设计出数据结构, 在施加以算法就行了。
所以,很重要的一点,数据结构和算法对建立解决问题的思想非常重要。
2.面试
这是很现实的一点,也是很多前端学习数据结构和算法的原因。
一般对待算法的态度会分为以下几类:
Google、Microsoft等知名外企在面试工程师时,算法是起决定性因素的,前端工程师也是一样,基本是每一轮都会考察,即使你有非常强的背景,也有可能因为一两道算法答的不好而与这样的企业失之交臂。
第二类,算法占重要因素的,国内的某些大厂在面试时,也会把数据结构和算法作为重要的参考因素,基本是面试必考,如果你达不到一定的要求,会直接挂掉。
第三类,起加分作用,很多公司不会把数据结构和算法作为硬性要求,但是也会象征性的出一些题目,当你把一道算法题答的很漂亮,这绝对是加分项。
如何准备
1.全方位了解
在学习和练习之前,你一定要对数据结构和算法做一个全方位的了解,对数据结构和算法的定义、分类做一个全面的理解,如果这部分做的不好,你在做题时将完全不知道你在做什么,从而陷入盲目寻找答案的过程,这个过程非常痛苦,而且往往收益甚微。
2.分类练习
当你对数据结构和算法有了一个整体的认知之后,就可以开始分类练习了。
注意,一定是分类练习!分类练习!分类练习!重要的事情说三遍。
所谓分类练习,即按每种类别练习,例如:这段时间只练习二叉树的题目,后面开始练习回溯算法的题目。
在开始练习之前,你往往还需要对这种具体的类别进行一个详细的了解,对其具体的定义、相关的概念和应用、可能出现的题目类型进行梳理,然后再开始。
3.定期回顾和总结
在对一个类型针对练习一些题目之后,你就可以发现一定的规律,某一些题目是这样解,另一些题目是那样解...这是一个很正常的现象,每种类型的题目肯定是存在一定规律的。
这时候就可以开始对此类题目进行总结了,针对此类问题,以及其典型的题目,发现的解题方法,进行总结。当下次你再遇到这种类型的题目,你就能很快想到解题思路,从而很快的解答。
所以,当你看到一个题目,首先你要想到它属于哪种数据结构或算法,然后要想到这是一个什么类型的问题,然后是此类问题的解决方法。
如果你看到一个新的问题还不能做到上面这样,那说明你对此类题目的掌握程度还不够,你还要多花一些经历来进行练习。
数据结构
什么是数据结构?
例1:如何在书架摆放图书。图书摆放需要解决2个问题:一是放书(新书怎么插入),另一个是找书(怎么找到某本指定的书)。
方法1:随便放
方法2:按书名的拼音字母顺序排放
方法3:按分类+拼音字母顺序放:把书架划分成几块区域,每块区域指定摆放某种类别的图书,在每种类别内,按照书名的拼音字母顺序排放
问题:书架空间怎么分配?类别分多细比较好?
例2:实现一个函数,传入一个正整数N后,依次打印数字0-N的正整数。
// 方法1
function printN(n) {
for(let i=0; i <= n; i++) {
console.log(i)
}
}
// 方法2
function printN(n) {
if(n) {
printN(n - 1)
console.log(n)
}
return ;
}
// 测试
function countTime(n) {
console.time()
printN(n)
console.timeEnd()
}
例3:实现一个函数,计算给定多项式在给定点__x__处的值:
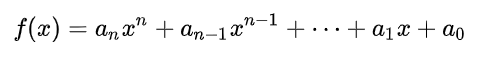
// 方法1 普通实现
function f(n, a, x) {
let i
let p = a[0]
for( i = 1; i <= n; i++ ) {
p += (a[i] * Math.pow(x, i))
}
return p
}
// 方法2 秦九韶算法
function f(n, a, x) {
let i
let p = a[n]
for( i = n; i > 0; i--) {
p = a[i - 1] + x*p
}
return p
}
// 测试
function testF(n = 5) {
console.time()
const a = []
const x = 2
for(let i = 0; i <= n; i++) {
a.push(i)
}
f(n, a, x)
console.timeEnd()
}
所以到底什么是数据结构?
数据对象在计算机中的组织方式
逻辑结构
物理存储结构
数据对象必定与一系列加在其上的操作相关联
完成这些操作所用的方法就是算法
逻辑结构
逻辑结构就是数据之间的关系,逻辑结构大概统一的可以分成两种:线性结构、非线性结构。
线性结构:是一个有序数据元素的集合。 其中数据元素之间的关系是一对一的关系,即除了第一个和最后一个数据元素之外,其它数据元素都是首尾相接的。
常用的线性结构有: 栈,队列,链表,线性表。
非线性结构:各个数据元素不再保持在一个线性序列中,每个数据元素可能与零个或者多个其他数据元素发生联系。
常见的非线性结构有 二维数组,树等。
存储结构
逻辑结构指的是数据间的关系,而存储结构是逻辑结构用计算机语言的实现。常见的存储结构有顺序存储、链式存储、索引存储以及散列存储。
例如:数组在内存中的位置是连续的,它就属于顺序存储;链表是主动建立数据间的关联关系的,在内存中却不一定是连续的,它属于链式存储;还有顺序和逻辑上都不存在顺序关系,但是你可以通过一定的方式去放问它的哈希表,数据散列存储。
抽象数据类型
用于描述数据结构的方法。
数据类型
数据对象集
数据集合相关联的操作集
抽象:描述数据类型的方法不依赖于具体实现
与存放数据的机器无关
与数据存储的物理结构无关
与实现操作的算法和编程语言均无关
只描述数据对象集和相关操作集”是什么”,并不涉及”如何做到“的问题。

问题: Vue 模板编译阶段为什么要用栈来检查标签是否正常闭合;
算法
定义
一个有限指令集
接受一些输入(有些情况下不需要输入)
产生输出
一定在有限步骤之后终止
每一条指令必须
有充分明确的目标,不可以有歧义
计算机能处理的范围之内
描述应不依赖于任何一种计算机语言以及具体的实现手段
算法分类
排序、查找、广度优先搜索、深度优先搜索、回溯算法、动态规划、贪心算法
时间复杂度和空间复杂度
我们首先要搞懂时间复杂度和空间复杂度的概念,它们的高低共同决定着一段代码质量的好坏:
时间复杂度
一个算法的时间复杂度反映了程序运行从开始到结束所需要的时间。把算法中基本操作重复执行的次数(频度)作为算法的时间复杂度。
没有循环语句,记作O(1),也称为常数阶。只有一重循环,则算法的基本操作的执行频度与问题规模n呈线性增大关系,记作O(n),也叫线性阶。
常见的时间复杂度有:
O(1): Constant Complexity: Constant 常数复杂度O(log n): Logarithmic Complexity 对数复杂度O(n): Linear Complexity 线性时间复杂度O(n^2): N square Complexity 平⽅方O(n^3): N square Complexity ⽴立⽅方O(2^n): Exponential Growth 指数O(n!): Factorial 阶乘

空间复杂度
一个程序的空间复杂度是指运行完一个程序所需内存的大小。利用程序的空间复杂度,可以对程序的运行所需要的内存多少有个预先估计。
一个程序执行时除了需要存储空间和存储本身所使用的指令、常数、变量和输入数据外,还需要一些对数据进行操作的工作单元和存储一些为现实计算所需信息的辅助空间。
