二叉树
什么是二叉树?
二叉树有什么类型?
二叉树有什么用?
具体实现
什么是二叉树
树是一种数据结构,由n个节点构成的具有层次关系的有限集合。
树的基本术语
节点:树中每个元素都是一个节点
节点的度:节点子树的个数
树的度:树中所有节点最大的度
叶子节点:度为0的节点(没有子节点的节点)
节点的层次:树的根开始,树根所在为第一层
有序树和无序树:子树有左右之分(如左边比右边大),反之则为无序树(例如大顶堆、小顶堆)
...
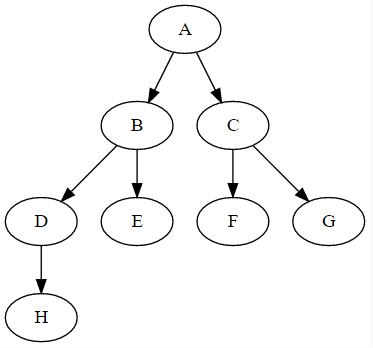
上图中
A 、B、...都为节点其中节点
A、B、C的度为2,D节点的度为1,H、E、F、G节点的度为0树的度为2
H、E、F、G为叶子节点其中节点
H为第4层,B为第二层
树的特点
子树不相交
除根节点外,所有节点都有且仅有一个父节点
由
N个节点构成的树只有N-1条边
二叉树的定义
所有节点的度不超过2的有序树
二叉树的特点
二叉树中,第
i层的节点最多为$ 2^{i-1}$个深度为
k的二叉树,最多 $ 2^k-1$个节点对任意的二叉树,叶子节点数量总比度为2的节点多一个
证明:
设度为0、1、2的节点个数分别为$ n_0、n_1、n_2$,共$n$个节点
因为二叉树所有节点的度不超过2,所以
n=n0+n1+n2
因为总节点数等于子节点总数加跟节点,所以
$$
n = 0 * n_0 + 1 * n_1 + 2 * n_2 + 1 \
n = n_1 + 2n_2 + 1 \
n_0 + n_1 + n_2 = n_1 + 2n_2 + 1 \
n_0 = n_2 + 1
$$
二叉树有什么类型
满二叉树
二叉树中除了叶子节点,每个节点的度都为2,则此二叉树为满二叉树
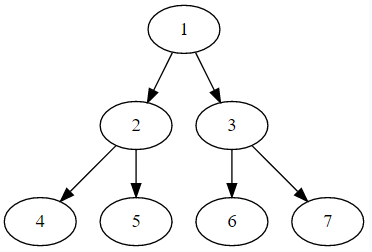
附加性质
满二叉树中第
i层的节点数为$ 2^{n-1} $个深度为
k的满二叉树必有$ 2^k - 1 $个节点,叶子节点树为$ 2^{k-1} $满二叉树中不存在度为 1 的节点,每一个分支点中都两棵深度相同的子树,且叶子节点都在最底层
具有
n个节点的满二叉树的深度为$ log_2 (n+1) $。
完全二叉树
二叉树中除去最后一层节点为满二叉树,且最后一层的结点依次从左到右分布
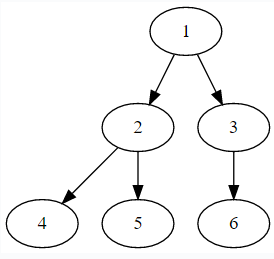
附加性质
n个节点的完全二叉树深度为$ \lfloor log_2n \rfloor + 1 $
...
二叉树有什么用
排序
搜索
...
搜索
约定:任一节点比其左节点大,比其右节点小
在上述约定下,二叉查找树的查找性能比链表高,一般有$ n $个节点的二叉查找树,其查找时间复杂度为$ O(log_2n) $
二叉树的查找操作
在二叉查找树中查找 N ,首先从根节点开始,将根节点设置为当前节点,若当前节点为空,则查找失败,若 N 与当前节点值相等,返回当前节点,若 N 大于当前节点值,则从当前节点的右子节点开始查找,否则从当前节点的左子节点开始查找,直到返回目标节点或者查找失败;
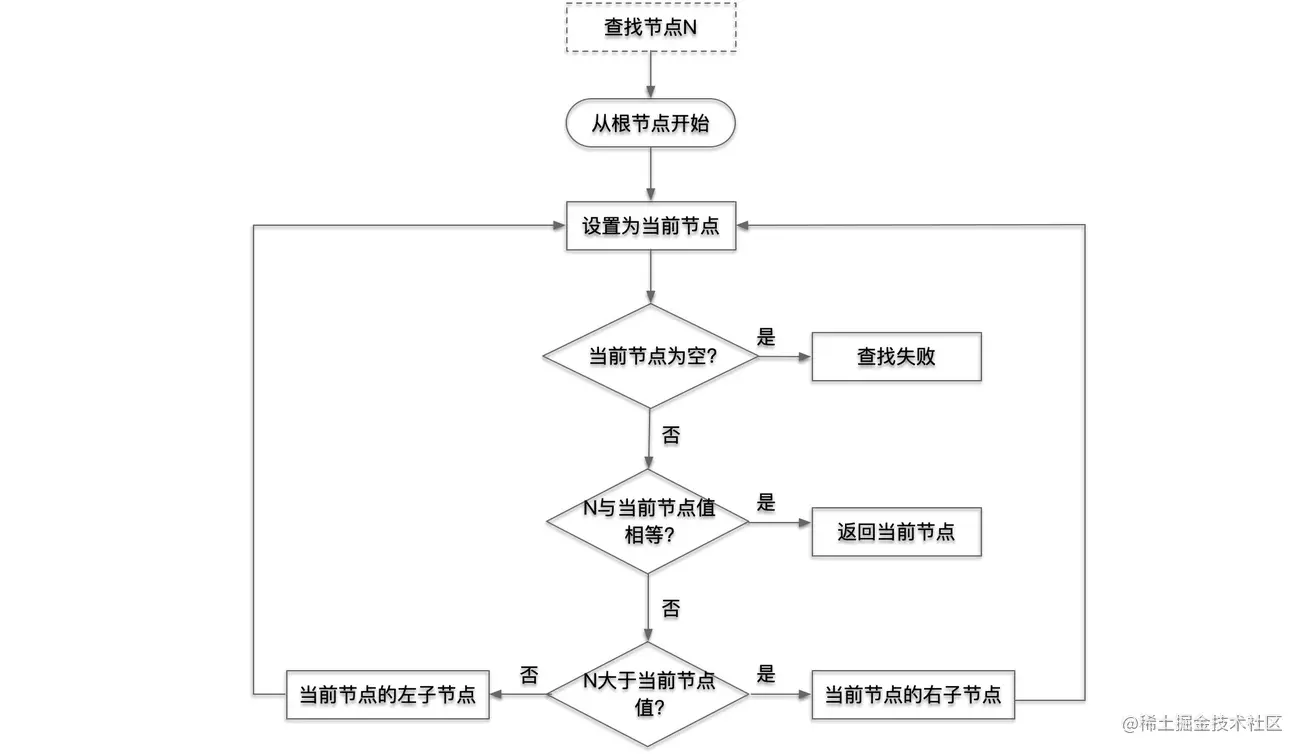
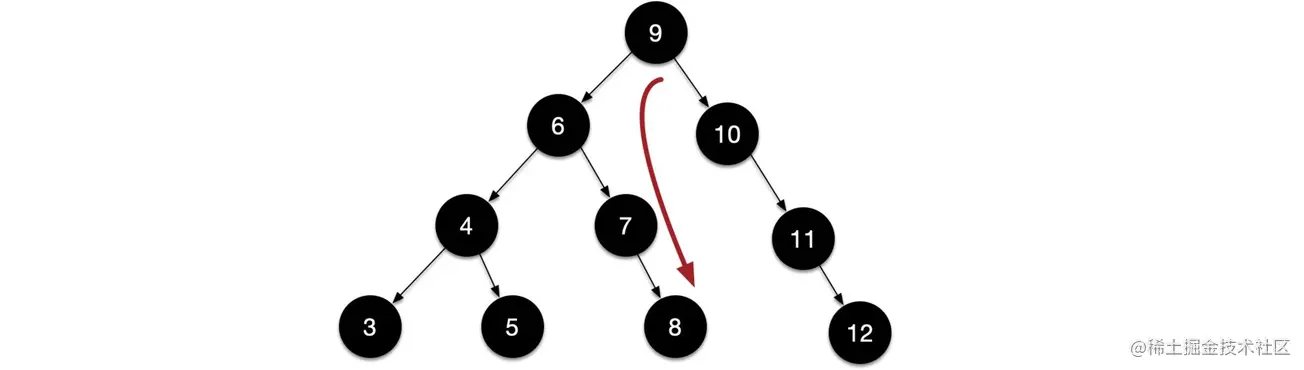
如下图在二叉查找树中查找目标 8 ,查找路径依次为 ⑨ --> ⑥ --> ⑦ --> ⑧
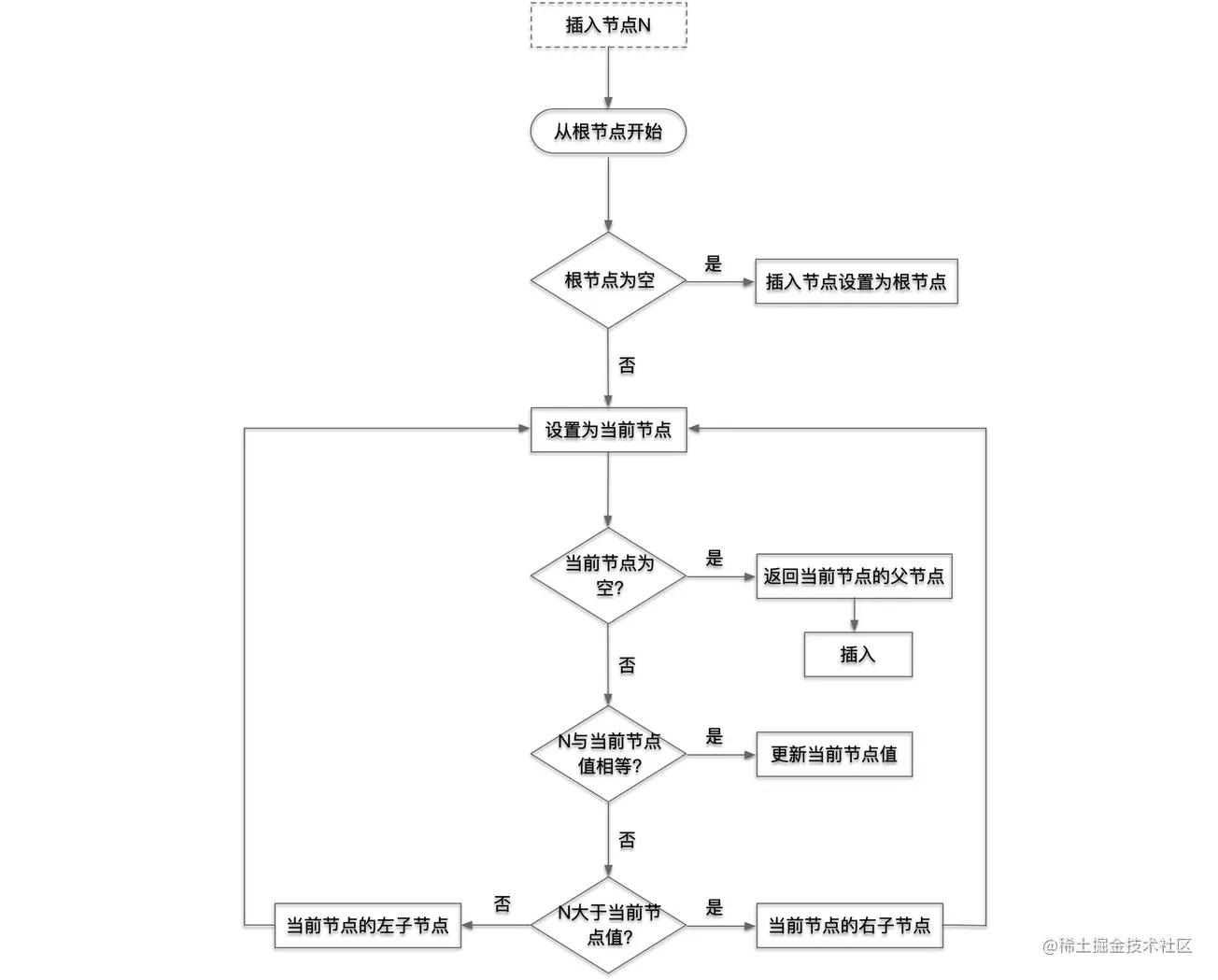
二叉树的构建
根据查找操作找到最合适的节点
在最合适的节点左边或右边插入
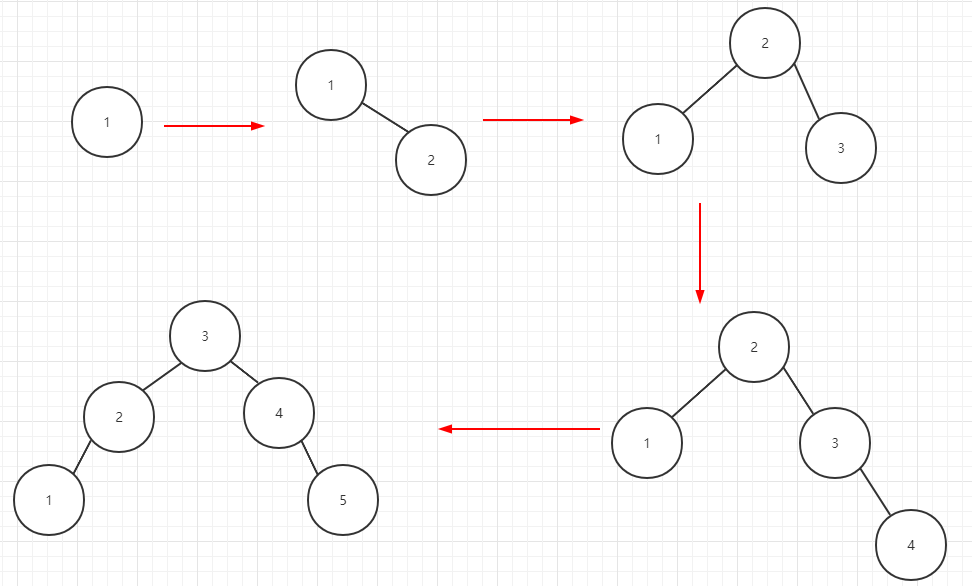
插入顺序为1、2、3、4、5
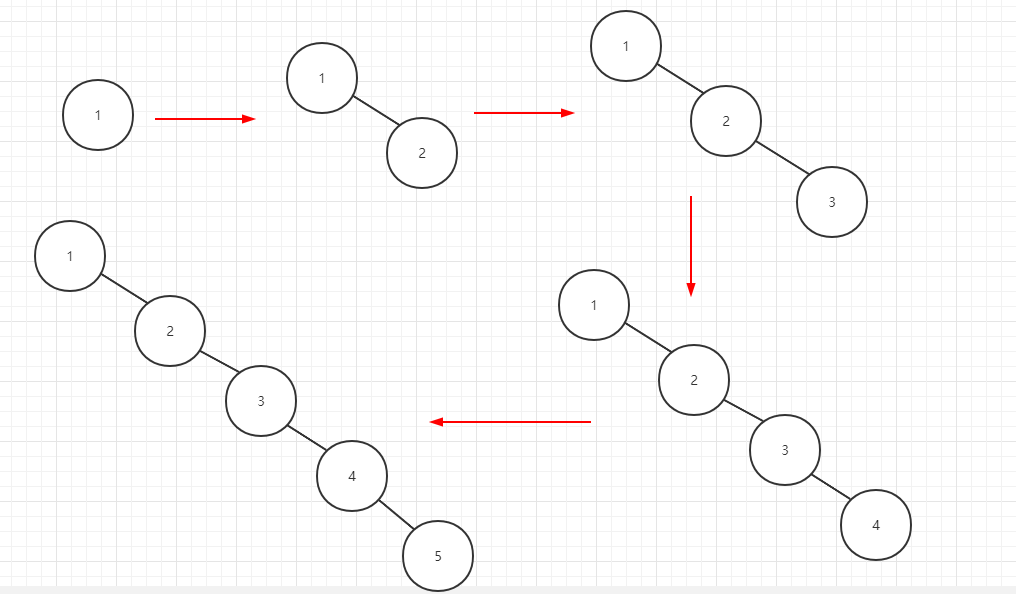
自平衡树
普通的二叉树查找树在构建时容易退化成链表,即不平衡二叉树,这样在增删查时无法彰显优势
进一步优化二叉查找树让其变成平衡二叉树,增加约定
所有节点的左右子树高度差不超过1
当左子树比右子树高2个及以上高度时,右旋
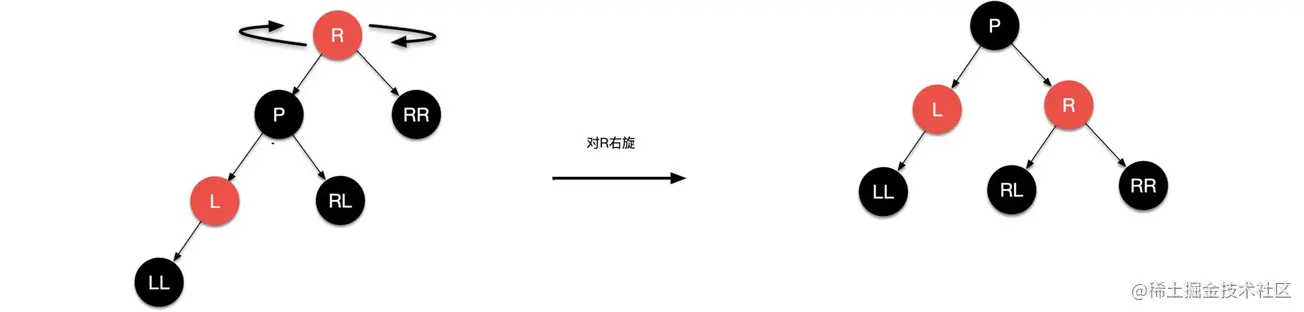
- 当右子树比左子树高2个及以上高度时,左旋
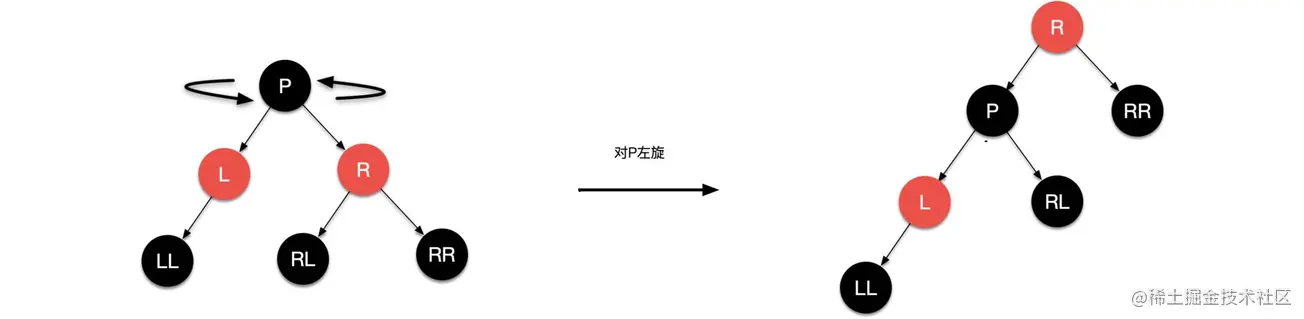
对插入顺序为1、2、3、4、5,其二叉树如下图